Existe, sin embargo, una observación experimental: en la superficie de la tierra todos los cuerpos caen en el vacío hacia el suelo con la misma aceleración (g). Sea un cuerpo cualquiera en la superficie de la tierra; su peso es:
donde Mg y mg son las masas respectivas (gravitatorias) de la Tierra y del cuerpo, R es el radio de la tierra (suponemos el cuerpo a una altura h pequeña, por lo que R + h ô R), y G es la constante de la gravitación universal.
Empleando la segunda ley de Newton, se puede relacionar el peso con la aceleración que experimenta el cuerpo:
w = mig;
Empleando la segunda ley de Newton, se puede relacionar el peso con la aceleración que experimenta el cuerpo:
w = mig;
siendo mi la masa (inercial) del mismo. Igualando ambas expresiones de w se obtiene:
Así, el cociente mi/mg permanece constante. Ya que G es una constante cuyo valor puede ser cualquiera, es posible elegir el mismo de forma que este cociente sea la unidad. De esta forma, ambas masas tendrían siempre igual valor:
mi ≡ mg
mi ≡ mg
Para ello, el valor de la constante de la gravitación universal ha de ser:
Consideraciones sobre el universo.— Supongamos que el universo tiene un tamaño finito, y que, de forma aproximada, se puede idealizar como una esfera, con una distribución de masa de densidad media r. Sea un cuerpo de masa m, situado a una distancia R del centro de dicha esfera; este experimentaría una fuerza atractiva hacia el centro del universo de valor:
Así, todos los cuerpos del universo experimentarán una aceleración hacia el centro de aquél de valor creciente proporcionalmente a su distancia R. Si esto fuese así, desde un punto distinto del centro del universo se observaría un movimiento diferente de las estrellas y galaxias según las distintas direcciones de observación; en la dirección del radio creciente, la aceleración sería mayor, mientras que en la opuesta disminuiría. Sin embargo, esto no parece concordar con las observaciones experimentales medidas desde la Tierra.
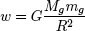




No hay comentarios:
Publicar un comentario