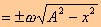Este es un video de ejemplo de movimientos armonicos simples aparecen varios experimentos espero y les agrade
jueves, 11 de junio de 2009
Oscilador Armonico Simple
Es el de un móvil que pasa cada cierto instante por las mismas posiciones.
Se dice que el móvil ha efectuado una oscilación cuando se encuentra en la misma posición que la de partida y moviéndose en el mismo sentido.
Se dice que el móvil ha efectuado una oscilación cuando se encuentra en la misma posición que la de partida y moviéndose en el mismo sentido.
Podemos definir entonces:
Periodo (T): tiempo que tarda en producirse una oscilación.
Frecuencia (f): número de oscilaciones que se producen cada segundo.
Periodo (T): tiempo que tarda en producirse una oscilación.
Frecuencia (f): número de oscilaciones que se producen cada segundo.
Movimiento oscilatorio armonico.
Si un cuerpo es apartado de su posición de equilibrio estable, comienzan a actuar sobre él fuerzas restauradoras que tienden a devolverlo a su estado original de equilibrio.
Si dicha fuerza recuperadora obedece la Ley de Hooke:
(es decir: dicha fuerza es proporcional a la posición de la partícula y tiende a llevarla hacia una posición de equilibrio considerada como x=0), entonces la posición de la partícula es una función sinusoidal del tiempo: decimos que dicha partícula está animada de un movimiento armónico simple. Y esta posición se puede escribir:
(es decir: dicha fuerza es proporcional a la posición de la partícula y tiende a llevarla hacia una posición de equilibrio considerada como x=0), entonces la posición de la partícula es una función sinusoidal del tiempo: decimos que dicha partícula está animada de un movimiento armónico simple. Y esta posición se puede escribir:
(I)x(t)= elongación: posición de la partícula respecto de la posición de equilibrio (x=0).
A: amplitud: máxima elongación: máxima distancia de la partícula a la posición de equilibrio.
: frecuencia angular:
: fase
: fase inicial
A partir de la expresión (I), derivando, podemos obtener las expresiones para la velocidad y aceleración de una partícula sometida a este movimiento:
A: amplitud: máxima elongación: máxima distancia de la partícula a la posición de equilibrio.
: frecuencia angular:
: fase
: fase inicial
A partir de la expresión (I), derivando, podemos obtener las expresiones para la velocidad y aceleración de una partícula sometida a este movimiento:
Además, es evidente comprobar que (I) es la solución para el movimiento de una partícula sometida a una fuerza recuperadora que obedece la Ley de Hooke:
y, como acabamos de ver 
, por tanto:
, que se cumple siem$pre que se haya definido 
.Energia Del M.A.S.
Toda partícula sometida a un movimiento armónico simple posee una energía mecánica que podemos descomponer en: Energía Cinética (debida a que la partícula está en movimiento) y
Energía Potencial (debida a que el movimiento armónico es producido por una fuerza conservativa).
Si tenemos en cuenta el valor de la energía cinética Ec = 1/2.m.v2 y el valor de la velocidad del m.a.s. obtenido en la ecuación del apartado cinemática,
v = dy/dt = A.w cos (w.t + Fo)
sustituyendo obtenemos
Ec = 1/2.m.v2 = 1/2.m.A2.w2.cos2 (w.t + Fo)
Ec = 1/2.k.A2.cos 2(w.t + Fo)
a partir de la ecuación fundamental de la trigonometría: sen2 + cos2 = 1
Ec = 1/2.k.A2.[ 1 - sen 2(w.t + Fo)]
Ec = 1/2.k[ A2 - A2sen 2(w.t + Fo)]
de donde la energía cinética de una partícula sometida a un m.a.s. queda
Ec = 1/2.k[ A2 - y2]
En donde observamos que tiene un valor periódico, dependiendo del cuadrado de la amplitud y del cuadrado de la elongación, obteniéndose su valor máximo cuando la partícula se encuentra en la posición de equilibrio, y obteniéndose su valor mínimo en el extremo de la trayectoria.
La energía potencial en una posicióny vendrá dada por el trabajo necesario para llevar la partícula desde la posición de equilibrio hasta el punto de elongación y.
Por ello el valor de la energía potencial vendrá dado por la expresión
Ep = 1/2.k.y2
Teniendo en cuenta que la energía mecánica es la suma de la energía potencial (9) más la energía cinética, nos encontramos que la energía mecánica de una partícula que describe un m.a.s. será:
E = 1/2.k.A2
En el m.a.s. la energía mecánica permanece constante si no hay rozamiento, por ello su amplitud permanece también constante.
Energía Potencial (debida a que el movimiento armónico es producido por una fuerza conservativa).
Si tenemos en cuenta el valor de la energía cinética Ec = 1/2.m.v2 y el valor de la velocidad del m.a.s. obtenido en la ecuación del apartado cinemática,
v = dy/dt = A.w cos (w.t + Fo)
sustituyendo obtenemos
Ec = 1/2.m.v2 = 1/2.m.A2.w2.cos2 (w.t + Fo)
Ec = 1/2.k.A2.cos 2(w.t + Fo)
a partir de la ecuación fundamental de la trigonometría: sen2 + cos2 = 1
Ec = 1/2.k.A2.[ 1 - sen 2(w.t + Fo)]
Ec = 1/2.k[ A2 - A2sen 2(w.t + Fo)]
de donde la energía cinética de una partícula sometida a un m.a.s. queda
Ec = 1/2.k[ A2 - y2]
En donde observamos que tiene un valor periódico, dependiendo del cuadrado de la amplitud y del cuadrado de la elongación, obteniéndose su valor máximo cuando la partícula se encuentra en la posición de equilibrio, y obteniéndose su valor mínimo en el extremo de la trayectoria.
La energía potencial en una posicióny vendrá dada por el trabajo necesario para llevar la partícula desde la posición de equilibrio hasta el punto de elongación y.
Por ello el valor de la energía potencial vendrá dado por la expresión
Ep = 1/2.k.y2
Teniendo en cuenta que la energía mecánica es la suma de la energía potencial (9) más la energía cinética, nos encontramos que la energía mecánica de una partícula que describe un m.a.s. será:
E = 1/2.k.A2
En el m.a.s. la energía mecánica permanece constante si no hay rozamiento, por ello su amplitud permanece también constante.
miércoles, 10 de junio de 2009
miércoles, 3 de junio de 2009
Movimiento armónico simple
Check out this SlideShare Presentation:
Movimiento armónico simple
View more OpenOffice presentations from Yuri Milachay.
Suscribirse a:
Entradas (Atom)
